Laurent Swhwartz

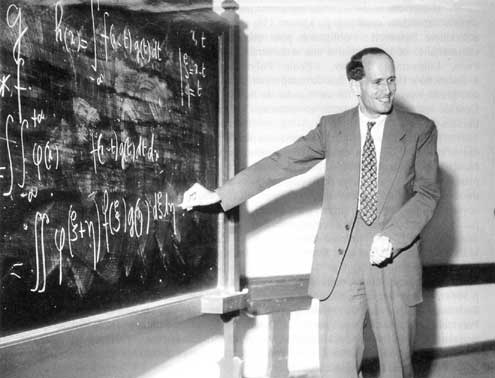J’ai eu la grande chance d’appartenir à la « fameuse promotion 1963 » de l’École polytechnique, dont Laurent Schwartz écrit dans ses Mémoires qu’elle fut celle qui lui a donné « le plus de bonheur ». En sont notamment issus plusieurs mathématiciens renommés.
Mon premier contact avec mon futur professeur puis collègue fut indirect. C’était l’été 1963, juste avant mon incorporation à l’X (à l’époque à la montagne Sainte-Geneviève). Nous passions nos vacances à Acquigny, un petit village normand proche de Louviers, où mes parents avaient hérité de la maison de campagne de ma grand-mère maternelle, un écrivain qui avait connu son heure de gloire dans l’entre-deux-guerres, sous le nom de plume d’André Corthis . Le général Cazelles, à l’époque le commandant de l’École polytechnique – on ne disait pas encore « directeur général » –, était dans la région. Nous nous étions rencontrés un soir chez le baron d’Esneval, propriétaire du joli château d’Acquigny. Je fus donc présenté au général comme un futur élève de notre grande école. Très rapidement la conversation tomba sur Laurent Schwartz. C’était le moment de sa réintégration après son exclusion à la suite de l’affaire du « manifeste des 121 », en 1960. Le général Cazelles m’expliqua à quel point le cours de Laurent Schwartz était impressionnant. Mais il ajouta aussitôt qu’il fallait prendre garde car le maître donnait l’illusion d’une grande facilité. En réalité, son cours était d’un niveau extrêmement élevé. Très peu, en fait, y comprenaient quelque chose. « Et donc, mon jeune ami, vous serez sûrement ébloui, mais vous serez probablement incapable de le suivre. » Comment, d’ailleurs, pouvait-on comprendre un bourbakiste ? Tel était en effet le cliché de l’époque. Je devais rapidement me rendre compte que le général Cazelles, au demeurant un homme fort honorable, raisonnait comme la masse des élèves « moyens » face à un cours d’une grande ambition.
L’École polytechnique, à cette époque, était renaissante. D’importantes réformes avaient été mises en place après 1956, Louis Armand étant devenu président du conseil d’administration. Dans ce contexte, le physicien Louis Michel et le mathématicien René Deheuvels, tous deux maîtres de conférences à l’X, étaient allés trouver Schwartz pour l’inciter à se porter candidat à la succession de Paul Lévy, arrivé à l’âge de la retraite en 1958. Dans les décennies précédentes, malgré son déclin relatif, l’enseignement de l’École avait bénéficié de mathématiciens de tout premier plan, comme Jacques Hadamard et Paul Lévy en analyse, ou Gaston Julia en géométrie. Mais leurs cours étaient d’une facture traditionnelle . Je note incidemment qu’Hadamard était un grand-oncle de Schwartz (le mari d’une sœur de sa grand-mère maternelle), et Lévy son beau-père. Ces liens ont dû jouer un rôle au moins marginal dans la décision du découvreur (c’est à dessein que je choisis ce terme, plutôt que celui d’inventeur) de la théorie des distributions. La question était maintenant de savoir si l’X allait prendre le tournant des mathématiques « modernes ». L’école mathématique française, encore illustre au début du XXe siècle avec des savants comme Gaston Darboux, Émile Picard, Paul Painlevé, Jacques Hadamard, Élie Cartan, René Baire, Émile Borel, Henri Lebesgue et, bien sûr, le génial Henri Poincaré, avait profondément souffert des ravages de la Grande Guerre. Au milieu des années 1930, le projet Bourbaki était né d’un objectif initialement assez modeste : remplacer dans l’enseignement supérieur les manuels existants, manifestement insuffisants, à commencer par le traité d’analyse d’Édouard Goursat . À la Faculté des sciences de Paris, il fallut attendre le remplacement de Georges Valiron par Gustave Choquet, en 1954, pour rénover drastiquement l’enseignement. Quelques années après, l’arrivée à l’X de Schwartz  membre important du groupe Bourbaki  constitua une véritable révolution.
À l’époque, recherche et enseignement étaient largement découplés à l’École polytechnique, à l’exception de la physique avec le laboratoire de Louis Leprince-Ringuet. Le corps enseignant était inégal, mais comptait quelques professeurs remarquables. En ce temps-là, l’alternance des promotions dites « jaunes » et « rouges » (la nôtre était « jaune »), se traduisait par celle du corps enseignant, c’est-à-dire que les professeurs faisaient cours une année sur deux. La promotion 1963 eut la chance d’avoir Laurent Schwartz en analyse. Les promotions « rouges » avaient Jean Favart . En mécanique, notre professeur fut Jean Mandel, qui décéda tragiquement quelques années plus tard. Il était excellent chercheur et très bon pédagogue. Je garde aussi un grand souvenir d’Emmanuel Grison, qui donnait un cours de chimie physique. Plus tard (de 1978 à 1984), il fut un merveilleux directeur de l’enseignement et de la recherche. En géométrie, nous eûmes droit à un amphi unique de Gaston Julia. Dans cet amphi, naturellement, ce grand blessé de la Grande Guerre ne faisait pas de mathématiques, mais il racontait tous les ans la même histoire, sur les conditions dans lesquelles il avait fait sa thèse avec l’illustre Charles Hermite. Le cours de Julia, astucieux mais décalé, nous était présenté par des maîtres de conférences dont aucun ne m’a marqué. En physique, le chef d’orchestre était Louis Leprince-Ringuet, une figure emblématique connue du grand public. Une grande partie des amphis était donnée par des maîtres de conférences, certains réputés pour la qualité de leurs travaux. Il y avait aussi de moins bons professeurs. C’est ainsi que nous dûmes subir l’anti-Schwartz, un ingénieur du Génie maritime chargé d’enseigner les probabilités. Le malheureux, qui officiait toujours en grand uniforme, était plein de bonne volonté, mais il n’y connaissait pas grand-chose, et j’en garde le pénible souvenir du plus mauvais professeur que j’aie jamais eu, celui qui avait l’art de rendre incompréhensibles les choses les plus simples, donc très exactement l’inverse du talent de Laurent Schwartz. Je n’ai hélas pas eu la chance de bénéficier des cours de mes futurs collègues Jacques-Louis Lions, Michel Métivier et Jacques Neveu qui devaient par la suite transformer l’enseignement des « mathématiques appliquées ».
Tout bien compris, Schwartz représentait pour nous un changement radical, un fantastique appel d’air, et cela devait avoir des conséquences profondes et durables sur la totalité de l’enseignement de l’École polytechnique.
La rentrée 1963 commençait, comme pour toutes les promotions de l’époque, par un stage militaire au camp des Garrigues. Une fois rentrés à l’école, ce qui nous a le plus motivés, ce qui a enthousiasmé ceux d’entre nous qui étaient réellement intéressés par les sciences et particulièrement par les mathématiques, ce fut évidemment le cours de Schwartz. Ce cours consistait en quarante leçons réparties sur la première année, ce qui en faisait une par semaine en moyenne. Quarante leçons, c’était peu par rapport à l’ampleur du programme. En cela, il n’y avait d’ailleurs rien de nouveau. Dans l’avant-propos de son traité, Jacques Hadamard évoque déjà les « exigences multiples et même quelque peu contradictoires qui s’imposent à pareil enseignement, à commencer par la condensation, la rapidité presque télégraphique d’un cours auquel le temps, comme dans toutes nos Grandes Écoles, est si parcimonieusement mesuré ». En taupe , on passait beaucoup de temps sur un programme peu étendu. À l’X, c’était l’inverse. Je ne crois pas, d’ailleurs, que les choses aient beaucoup changé sur ce point. Les deux tomes d’Hadamard n’avaient pas moins de mille trois cents pages d’une typographie serrée…
Pour revenir à Schwartz, la première chose qui frappait chez lui, c’était sa clarté. Une clarté admirable, qui justifiait son mythe, d’où la fausse idée de simplicité qu’il pouvait donner. Schwartz avait effectivement ce talent extraordinaire de rendre intelligible, avec un minimum d’efforts, les choses les plus complexes. La clarté n’est pas sans lien avec l’élégance. Elle a donc  comme l’invention, j’y reviendrai  une dimension esthétique. Pour Schwartz, il y avait le timbre de sa voix, sa fameuse voix, sa manière de parler, le rythme de sa phrase. Il y avait la beauté de son écriture, sur le papier comme au tableau noir. Sa manière très particulière d’onduler le long du tableau et d’écrire les équations avait quelque chose d’harmonieux, le rythme de la démarche répondant à celui de la voix et au mouvement de la craie. Il y avait la parole et le geste. Et donc ses amphis étaient physiquement fascinants.
Quelques-uns d’entre nous avaient proposé de faire des résumés écrits de ses cours. Nous fûmes une dizaine à nous répartir le travail. Après chaque amphi, nous rédigions en quelques pages ce qui avait été traité. Le maître validait ces résumés, qui étaient ensuite diffusés à toute la promotion, facilitant la tâche d’une grande majorité d’élèves.
Après la clarté, le style. Tout travail humain a un style. Écoutons David Ruelle : « Vous visitez un musée de peinture, et vous vous promenez parmi les toiles françaises du début du XXe siècle. Vous voyez ici un Renoir somptueux, là sans erreur possible c’est un Modigliani, là encore ce sont des fleurs peintes par Van Gogh, ou des fruits de Cézanne. Plus loin vous apercevez un Picasso, à moins que ce ne soit un Braque. Sans doute est-ce la première fois que vous voyez ces peintures, mais vous n’avez le plus souvent aucun doute quant à l’artiste à qui on les doit […]. De même, si vous ouvrez la radio, vous saurez immédiatement si vous entendez de la musique classique ou les Beatles. Et si la musique classique vous intéresse le moins du monde, vous reconnaîtrez Bach de la musique du XVIe siècle, Beethoven de Bach, et Bartok de Beethoven. Ce sont des morceaux que peut-être vous n’avez jamais entendus, mais il y a quelque chose d’unique dans l’arrangement des sons qui permet de reconnaître presque instantanément le compositeur. On peut essayer d’identifier ce “quelque chose d’unique” par des études statistiques . » S’agissant de littérature, de peinture, de sculpture, d’architecture, de musique, etc., ce « quelque chose d’unique » est ce que l’on appelle communément le style. Je crois que la notion de style vaut aussi pour les sciences. Ainsi, le style de Richard Feynman dans ses célèbres Lectures on Physics a-t-il marqué plusieurs générations d’étudiants.
Laurent Schwartz avait un style bien à lui. Si vous prenez au hasard quelques pages de traités d’analyse français contemporains, par exemple Dieudonné, Schwartz ou Godement, vous n’aurez aucune difficulté à en identifier les auteurs. Le style de Schwartz tient dans une manière d’écrire qui coule, si je puis dire, comme à l’oral ; un choix de notations (en mathématiques, les notations font partie de l’écriture  il y a à la fois un aspect esthétique et un aspect d’économie de pensée ) ; mais aussi et peut-être surtout une « tonalité » dans l’arrangement des matières traitées. C’est là que la « forme » rejoint le « fond ». À cet égard, le style de Schwartz, dans son enseignement, est évidemment bourbakique, mais avec deux nuances importantes. La première est que, tout en raisonnant du général vers le particulier et en privilégiant les structures, il ne recherche jamais systématiquement le plus haut degré de généralité possible, quitte à augmenter le caractère « fouillis » de l’ensemble. Ainsi la topologie est-elle disséminée tout au long du cours, à mesure que le besoin peut s’en faire sentir. La seconde nuance concerne les applications. Schwartz en avait le souci, manifeste aussi dans sa propre recherche, à commencer par la théorie des distributions qui trouve son origine dans le calcul symbolique de Heaviside, un ingénieur électricien du XIXe siècle, et dans les travaux de Dirac, motivés par la physique théorique, au début du XXe. Schwartz a d’ailleurs donné à la Faculté de sciences de Paris un enseignement très original pour l’époque de « méthodes mathématiques pour les sciences physiques » .
Globalement, cependant, la préoccupation structurelle dominait, peut-être aux dépens de connaissances directement utilisables pour la résolution des problèmes rencontrés dans les diverses disciplines. De ce point de vue, le style de Schwartz était très différent de celui d’un Hadamard, qu’il qualifiait affectueusement de « poule à théorème » mais n’avait aucune grande construction théorique à son actif. En tout cas, les équations aux dérivées partielles par exemple  qui occupent une place importante dans les cours plus anciens, dont celui d’Hadamard  n’étaient pas abordées faute de temps, alors qu’elles sont omniprésentes en physique.
Le style, c’est aussi une certaine manière de raisonner. Je me souviens à ce sujet d’une conversation où Schwartz m’avait dit : « il y a deux sortes de mathématiciens ; il y a ceux, comme Dieudonné, qui lisent les mathématiques à livre ouvert, qui comprennent tout instantanément et absorbent immédiatement les démonstrations ; et puis il y a les gens comme moi, qui ont du mal à lire une démonstration jusqu’au bout, vont tout de suite au résultat, et essayent de le démontrer par eux-mêmes. » Ceux-là se battent avec les théorèmes, et c’est seulement ensuite, s’ils ne s’en sortent pas, que, la mort dans l’âme, ils se résignent à regarder les démonstrations. À la réflexion, la manière de parler et d’écrire de notre héros se ressentait de cette caractéristique. Je crois que la distinction établie par Schwartz ne vaut pas seulement dans les mathématiques. Quel que soit le domaine, il y a ceux qui absorbent comme des éponges et ceux qui, en quelque sorte, se situent toujours en position d’invention. Plus tard, je devais retrouver chez d’autres grands auteurs la distinction sur laquelle Schwartz avait attiré mon attention. Ainsi Paul Montel fait-il cette observation dans la préface qu’il a donnée à l’ouvrage posthume d’Henri Lebesgue sur les coniques : « Sans doute, Lebesgue aurait désiré fondre en un seul les trois articles qui constituent [le chapitre I]. L’exposition y eût gagné en unité et en concision et la lecture en eût été plus aisée. Elle aurait été aussi moins instructive ; la forme présente permet de suivre la marche d’une pensée pénétrante et féconde ; elle laisse ouverte la possibilité de nombreux modes d’exposition. L’auteur souhaite que chaque lecteur, cessant de lire, édifie sa propre théorie. Il suit en cela une habitude qui lui est chère : Lebesgue n’a jamais pu lire un mémoire jusqu’au bout ; il a toujours essayé de le reconstruire à sa manière et de le penser à nouveau entièrement . » De ce point de vue, le caractère un peu fouillis du cours de Schwartz, distribué aux élèves sous forme de « feuilles », comme on disait alors, avait son bon côté, car il incitait davantage le lecteur dont le cerveau était construit comme le sien à se bagarrer avec le texte . Je relèverai encore un passage de l’autobiographie de Paul Lévy, dans un registre différent, mais voisin : « Je suis trop polarisé sur les problèmes qui m’occupent pour être ouvert aux idées des autres ; je ne lis qu’avec effort, et il peut m’arriver de sous-estimer l’intérêt d’un travail, s’il ne se rapporte pas au moins à un sujet qui m’ait autrefois intéressé . »
Après le style, abordons plus précisément le contenu. Le cours, donc, comprenait quarante séances réparties sur l’année. Après quelques compléments de théorie des ensembles, il commençait véritablement par un chapitre de topologie générale. La topologie était alors balbutiante dans les taupes, à quelques exceptions près, comme celle de Pierre Martin à Janson-de-Sailly, dont j’étais issu. Ce chapitre, qui comprenait près de deux cents pages, était largement centré sur les espaces métriques et les espaces de Banach. Je pense qu’il présentait déjà des difficultés sérieuses pour ceux qui provenaient (nous sommes au début des années 1960) des taupes les plus traditionnelles. Le troisième chapitre traitait du calcul différentiel, dans le cadre assez général des applications d’un espace affine normé dans un autre. Il comprenait une introduction aux variétés différentiables plongées dans un espace affine, et même quelques développements sur les variétés abstraites et sur le calcul des variations. Le gros morceau, c’était le calcul intégral. En raison de son tropisme pour l’analyse fonctionnelle, Schwartz avait choisi de présenter l’intégrale de Lebesgue  une notion qu’il était hors de question d’introduire en taupe à l’époque  à partir des mesures de Radon sur les espaces localement compacts, plutôt que par la voie des mesures dites abstraites. La théorie des distributions pouvait apparaître a posteriori comme une justification de ce choix. Mais pour la plupart des débutants, ce n’était sûrement pas la façon la plus intuitive de procéder, en particulier pour ceux qui voulaient aborder les probabilités. Pour un premier contact avec les probabilités, la voie de la mesure dite abstraite est certainement plus naturelle .
La progression était laborieuse. Pour arriver à la notion de mesure des ensembles, il fallait passer par de longs détours  les mesures extérieures des ouverts, les mesures intérieures des compacts, etc. Tout cela était un peu déroutant. On était emporté par la majesté de l’exposé, mais on ne voyait clairement ni l’objectif à atteindre, ni la stratégie sous-jacente. Une fois acquise la notion d’ensemble mesurable, on abordait la construction de l’intégrale proprement dite, mais il fallait encore subir de nombreuses étapes intermédiaires. On aboutissait enfin à un premier sommet de l’imposante construction, qui était le théorème de convergence dominée de Lebesgue. Et il restait encore à traiter les produits tensoriels de mesures, à appliquer tout cela aux intégrales multiples, à introduire la convergence des mesures, avec un retour à la topologie, etc. Tout cela, c’était le quatrième chapitre.
À ce stade de mon exposé, je rapporterai une expérience personnelle qui m’a profondément marqué. C’était, je crois, un jour de novembre 1963. Je me revois dans la bibliothèque de l’ancienne École polytechnique, rue Descartes, travaillant sur le chapitre en question. Je comprenais sans difficulté chaque lemme, théorème, corollaire, etc. pris individuellement ou même localement, mais le sens de la démarche dans son ensemble m’échappait. Soudain, en une fraction de seconde, j’éprouvai cette sensation extraordinaire que tout se mettait en place, qu’enfin je comprenais la théorie de la mesure, c’est-à-dire, au-delà de l’intelligence des briques élémentaires, que j’accédais à celle de l’édifice dans sa globalité, et donc de sa structure. Pour la première fois, je me représentais clairement que comprendre un objet d’attention, c’est s’en approprier la structure, c’est une incarnation, et que cela procède généralement par voie de « cristallisation », au terme d’un processus cérébral laborieux et mystérieux où l’inconscient joue un rôle décisif. Ce jour-là, il s’agissait de l’intégration, mais à des degrés divers d’intensité j’ai éprouvé la même sensation, dans la décennie de mes vingt ans, à propos par exemple de la théorie des probabilités ou, en physique, des mécaniques relativiste et quantique, et ultérieurement dans des domaines plus ou moins éloignés des sciences dures.
J’ai employé le mot « cristallisation », le plus propre selon moi à caractériser le phénomène dont je parle. Sur la terre, les atomes se déplacent constamment sous l’effet de toutes sortes de forces, et certains parviennent à « se trouver » pour initier un cristal, donc une structure qui se développe ensuite en obéissant au principe de la minimisation de l’énergie totale. Le tout est de commencer. On sait que Stendhal, dans un ouvrage écrit en 1820 intitulé De l’Amour, appelle cristallisation « l’opération de l’esprit, qui tire de tout ce qui se présente la découverte que l’objet aimé a de nouvelles perfections ». L’image lui était venue de l’observation d’un phénomène naturel : « Aux mines de sel de Hallein, près de Salzbourg, les mineurs jettent dans les profondeurs abandonnées de la mine un rameau d’arbre effeuillé par l’hiver ; deux ou trois mois après, par l’effet des eaux chargées de parties salines, qui humectent ce rameau et ensuite le laissent à sec en se retirant, ils le retrouvent tout couvert de cristallisations brillantes. Les plus petites branches, celles qui ne sont pas plus grosses que la patte d’une mésange, sont incrustées d’une infinité de petits cristaux mobiles et éblouissants. »
A première vue, l’idée de Stendhal s’applique à un autre type d’expérience que celui dont je parle. Et pourtant, les deux ne sont pas sans rapport. Dans sa célèbre conférence sur l’invention mathématique, Henri Poincaré dit ceci : « Les phénomènes inconscients privilégiés, ceux qui sont susceptibles de devenir conscients, ce sont ceux qui, directement ou indirectement, affectent le plus profondément notre sensibilité. On peut s’étonner de voir invoquer la sensibilité à propos de démonstrations mathématiques qui, semble-t-il, ne peuvent intéresser que l’intelligence. Ce serait oublier le sentiment de la beauté mathématique, de l’harmonie des nombres et des formes, de l’élégance géométrique. C’est un vrai sentiment esthétique que tous les vrais mathématiciens connaissent. Et c’est bien là de la sensibilité. Or, quels sont les êtres mathématiques auxquels nous attribuons ce caractère de beauté et d’élégance, et qui sont susceptibles de développer en nous une sorte d’émotion esthétique ? Ce sont ceux dont les éléments sont harmonieusement disposés, de façon que l’esprit puisse sans effort en embrasser l’ensemble tout en pénétrant les détails. Cette harmonie est à la fois une satisfaction pour nos besoins esthétiques et une aide pour l’esprit qu’elle soutient et qu’elle guide. Et en même temps, en mettant sous nos yeux un tout bien ordonné, elle nous fait pressentir une loi mathématique. […] De sorte que nous arrivons à la conclusion suivante : les combinaisons utiles, ce sont précisément les plus belles, je veux dire celles qui peuvent le mieux charmer cette sensibilité spéciale que tous les mathématiciens connaissent, mais que les profanes ignorent au point qu’ils sont souvent tentés d’en sourire. »
Dans une étude postérieure d’une trentaine d’années, également très connue, Jacques Hadamard s’interroge sur le choix des sujets de recherche (pour une thèse par exemple) en mathématiques, et donne la même réponse que Poincaré : « Le guide à qui nous devons nous fier est le sens de la beauté, cette sensibilité esthétique spéciale dont il a souligné l’importance. Comme le note [dans L’Avenir des sciences] également Renan (chose curieuse), il existe un goût scientifique, exactement comme il y a un goût artistique ou littéraire ; et ce goût peut être plus ou moins sûr selon les individus . »
Ainsi, de mon point de vue, l’emploi du mot cristallisation se trouve-t-il doublement justifié. S’agissant de l’invention ou de la découverte à proprement parler, Poincaré insiste longuement sur le travail de l’inconscient et le rôle de l’illumination, avec ses « caractères de brièveté, de soudaineté et de certitude immédiate ». Inventer, explique-t-il, « cela consiste précisément à ne pas construire les combinaisons inutiles et à construire celles qui sont utiles et qui ne sont qu’une infime minorité. Inventer, c’est discerner, et choisir. » « Inventer, c’est choisir », comme on dit : « gouverner, c’est prévoir ». Nous sommes là bien loin des illusions de la recherche opérationnelle des années 1970 et de l’exploration systématique des combinaisons. Dans les deux cas, l’essentiel est dans l’intuition et le « long travail inconscient antérieur ». Hadamard développe abondamment cet aspect de la création. Fulgurance, illumination, cristallisation, chacun choisira son mot préféré. Je serais tenté, sur un autre registre, d’y ajouter « conversion », cette discontinuité qui change une vie, comme l’expérience de saint Paul sur le chemin de Damas.
Laurent Schwartz était évidemment pénétré de ces réalités psychologiques. Il les exprimait avec une autre métaphore, celle de la percolation et, dans son autobiographie, on voit la percolation à l’œuvre dans son esprit avec la théorie des distributions, qu’il présente d’ailleurs comme une découverte et non comme une invention, une nuance fort importante du point de vue philosophique, à laquelle j’ai déjà fait allusion et sur laquelle je reviendrai encore une fois brièvement. « Certaines époques se prêtent plus que d’autres à une découverte complète. Quand je trouvai les distributions d’un seul coup, non seulement j’y étais préparé par mes réflexions précédentes, mais l’époque était très propice en raison des travaux antérieurs de nombreux mathématiciens. Si je ne les avais pas trouvées, il me paraît certain qu’on l’aurait fait dans les quelques années qui ont suivi. » Quant à la découverte elle-même, elle eut lieu, comme souvent, une nuit : « J’ai toujours appelé cette nuit de découverte ma nuit merveilleuse, ou la plus belle nuit de ma vie . »
Après cette longue parenthèse, revenons au cours et au chapitre V. Celui-ci portait sur les équations différentielles, avec les théorèmes d’existence et d’unicité, de prolongement, de continuité de la solution en fonction d’un paramètre, et le cas particulier des équations différentielles linéaires. Après le calcul intégral, ce chapitre-là paraissait extrêmement facile. Tout cela, c’était pour le premier semestre.
Le second semestre était encore plus grandiose, mais la rédaction des « feuilles » était moins construite, plus mélangée, et d’ailleurs elle n’a jamais été complètement achevée. Cela commençait par un formidable morceau de près de trois cents pages, sobrement intitulé « Calcul différentiel extérieur », débouchant naturellement sur la formule de Stokes en dimension quelconque, et même, pour les plus courageux, sur une impressionnante « application de la théorie des formes différentielles à la topologie algébrique ». Cette introduction à l’homotopie et à l’homologie n’a pas été reprise dans la publication du cours en quatre volumes ; car, à ce que l’auteur m’a dit lui-même, la construction péchait quelque part. Inutile de vous dire qu’à ma connaissance, même les meilleurs d’entre nous ne s’en étaient pas aperçus alors que, dans d’autres enseignements, il avait pu nous arriver de déceler des erreurs.
Suivait un chapitre encore très substantiel sur les fonctions de variables complexes, lesquelles étaient présentées à partir du précédent, ce qui n’était pas non plus forcément la voie la plus facile. C’est alors seulement que l’on abordait la théorie des distributions. Laurent Schwartz n’avait pas voulu en entreprendre une rédaction nouvelle. On le comprend ! Son grand ouvrage sur le sujet était évidemment d’un niveau trop élevé pour un cours à l’X (la principale difficulté concernant les espaces vectoriels topologiques), mais celui de son manuel Méthodes mathématiques pour les sciences physiques paraissait trop faible à certains d’entre nous. Nous avions brusquement l’impression de descendre de plusieurs étages. C’est dans ce cadre-là que nous abordions la série et l’intégrale de Fourier, ainsi que la transformation de Laplace. Il me fallut quelque temps  et en fait mon séjour ultérieur à Berkeley  pour admettre qu’il était bon de s’exercer à passer facilement d’un étage à un autre, et d’ailleurs aussi d’un auteur à un autre. Les étudiants français sont moins bien préparés que les Américains à cette gymnastique en réalité indispensable.
Je voudrais, avant de terminer cette revue de l’enseignement de Laurent Schwartz à l’Ecole polytechnique, faire quelques remarques à propos des distributions. Il y avait quelque chose d’exaltant à apprendre, de son propre découvreur, une théorie aussi récente et aussi féconde : la plus belle nuit de notre professeur datait de moins de vingt ans ! Nous étions bien préparés à comprendre qu’il était aussi naturel de généraliser les fonctions avec les distributions que de passer des nombres rationnels aux nombres réels. De plus, l’utilité de ces nouveaux objets paraissait éclatante. Pour ma part, j’en pris immédiatement conscience à partir d’un problème élémentaire d’électricité, sur lequel j’avais buté en mathématiques spéciales. Le programme de l’époque comprenait l’étude des galvanomètres à cadre mobile, appareils destinés à mesurer des courants très faibles. Le cadre porte quelques centaines de tours de fil de cuivre fin, et tourne autour de deux fils de suspension qui à la fois le supportent et lui amènent le courant. Ce dispositif est pris dans le champ magnétique radial d’un aimant en fer à cheval. On repère le mouvement du cadre par son élongation, c’est-à-dire l’angle qu’il fait avec sa position au repos. Cet angle obéit à une équation différentielle du second ordre à coefficients constants. Les coefficients du premier membre de l’équation dépendent des caractéristiques de l’appareil. Le second membre se réduit à l’intensité du courant qu’on y introduit. Dans le cas particulier du galvanomètre balistique, il s’agit de mesurer la quantité d’électricité qui le traverse pendant un temps très court, à partir du fait que l’élongation maximum du cadre est proportionnelle à la quantité d’électricité en question. Le problème consistait à démontrer ce fait. Le raisonnement du manuel de Lamirand et Joyal, sur lequel je travaillais, n’avait ni queue ni tête. J’avais écrit en marge « ridicule ! faux ! non-sens ! ». En taupe, j’ignorais tout, bien sûr, du « calcul symbolique » ; mais, si je l’avais connu, ma frustration n’aurait pas été moindre. N’ayant pas été capable de surmonter l’obstacle, quelle ne fut pas ma satisfaction, à l’X, de trouver la solution ! Il suffisait d’écrire l’intensité comme le produit de la quantité d’électricité par la dérivée de la distribution delta de Dirac, puis de résoudre l’équation au sens des distributions, où les techniques du « calcul symbolique » sont totalement justifiées. Tout cela était finalement très simple, et en tout cas naturel.
Avec les distributions, nous n’en avions pas terminé. Il y avait encore un traitement des espaces hilbertiens, une introduction à la théorie des opérateurs compacts et des opérateurs intégraux  tout cela pour nous « préparer » à la mécanique quantique , puis un appendice de quatre-vingts pages très denses sur la théorie des probabilités, pour suppléer sans le dire à la carence de l’enseignement de mathématiques appliquées dont j’ai parlé tout à l’heure ! Il est à peine utile de préciser que l’enseignement en question n’a pas pu résister bien longtemps à pareil choc.
En plus de tout cela, pour ceux qui le voulaient, Laurent Schwartz donnait un séminaire, auquel participaient une quinzaine d’élèves, ce qui était pour nous l’occasion de nouer un vrai contact avec lui.
Nous avions, je l’ai dit, quelques excellents professeurs et les disciplines qui nous étaient enseignées par ailleurs étaient souvent passionnantes. Néanmoins, pour les plus exigeants d’entre nous  il faut rappeler qu’à l’époque le concours d’entrée était unique, et la mathématique constituait de loin la matière dominante, et donc le premier critère de la sélection à l’entrée , le cours de Schwartz aplatissait les autres de manière plus ou moins sensible. Cela pouvait obscurcir notre jugement. Il est vrai par exemple qu’en physique nous n’avions pas l’équivalent de Schwartz, nous n’avions pas Feynman. Bernard Gregory, tout récemment nommé à la tête de l’Organisation européenne pour la recherche nucléaire (CERN), n’enseignait pas à notre promotion, hélas. Malgré tout, les cours de mécanique quantique, de physique atomique ou de physique statistique étaient d’une grande qualité. Ils donnaient même beaucoup de satisfactions à ceux qui, comme moi, avaient dévoré les ouvrages de vulgarisation de Louis de Broglie, Werner Heisenberg ou Louis Leprince-Ringuet avant d’entrer à l’X. Au début des années 1960, beaucoup d’acteurs de l’aventure atomique (au sens large du terme) étaient encore vivants, et nos cours de l’École nous permettaient de la toucher.
Ce qui toutefois nous gênait  du moins dans mon expérience et dans mon souvenir , c’était le style mathématique des physiciens. Je retrouvais, à grande échelle, le syndrome du galvanomètre balistique et du manuel de Lamirand et Joyal. Comment était-il possible d’enseigner à l’École polytechnique en ignorant la théorie des distributions et en faisant des espaces de Hilbert un usage aussi approximatif pour ne pas dire fantaisiste ? Il m’a fallu un certain temps pour admettre que cette manière de voir était injuste et surtout en partie inexacte. La culture des physiciens (ou des chimistes, ou des biologistes, etc.) en tant que communauté de savoir n’est pas celle des mathématiciens, parce que les uns et les autres n’appliquent pas leur intelligence aux mêmes objets. Pour les physiciens, les mathématiques ne sont qu’un outil que l’on utilise sans davantage se soucier de « rigueur », de même que la plupart des gens ne se préoccupent guère de la grammaire lorsqu’ils s’expriment dans la vie courante. Même un théoricien comme Dirac n’était pas embarrassé de jongler avec sa « fonction » delta, et il avait raison ! Physiciens et mathématiciens n’ont pas le même sens de l’esthétique, ils ne partagent pas les mêmes « goûts » intellectuels. À l’ère des ordinateurs, le développement de l’analyse numérique a jeté un pont entre les deux , mais ce pont, de l’ordre du pratique, ne saurait abolir la différence des sensibilités. D’un point de vue pratique, également, il en résulte que l’on n’enseigne pas les mathématiques de la même façon selon le point de vue de l’« utilisateur », un argument essentiel en faveur de la diversification de l’enseignement à l’X. Mais au début des années 1960, on en était encore à la conception traditionnelle de l’uniformité.
J’ajouterai, s’agissant du climat d’ensemble à l’École, que le succès et le prestige de Laurent Schwartz suscitaient beaucoup de jalousies. Mais nous étions bien jeunes et, à cet égard, inconscients. En tout cas, je l’étais.
Vint l’été 1964, au terme de cette inoubliable première année. Passionnés que nous étions, François Laudenbach et moi avons consacré une partie de nos vacances à travailler à la campagne sur une nouvelle rédaction du cours d’analyse, en partie avec Laurent Schwartz lui-même. Nous avons perdu toute trace de notre carburation. Mais j’ai le souvenir de conversations tout à fait passionnantes avec notre maître dont la bienveillance me frappait. Les professeurs ne devraient jamais oublier qu’ils peuvent avoir un impact extraordinaire sur leurs élèves, parfois même les éclairer une vie entière pour des raisons qui dépassent le contenu de leur enseignement. À mon entrée à l’X, j’avais  certes confusément  la vision naïve de la science comme un domaine fini, que l’on pouvait apprendre par transmission. L’idée d’une science se faisant, avançant même très vite, était étrangère à la culture des taupins. On nous présentait plus ou moins bien des temples achevés. Pendant les premiers mois du cours de Schwartz, je pris conscience avec effarement de l’immensité et surtout de la nature irréductible de mes lacunes. C’était bouleversant. Au fur et à mesure de l’avancée, je réalisais que le champ de mon ignorance identifiée progressait plus vite que celui de mes connaissances. Un jour où je méditais sur cette constatation, nous reçûmes la visite d’une promotion de cyrards. Cela faisait partie des traditions. Certains d’entre nous avaient mission de faire visiter l’École à des camarades de Coëtquidan. L’un d’eux me demanda ce que l’on nous enseignait. Bien sûr, je commençai par les maths. Mon interlocuteur s’exclama : « Quoi ? Vous ne savez donc pas toutes les maths en arrivant à l’X ? » Le contraste entre ce cri du cœur et ma propre expérience fut tellement fort que la scène reste gravée dans ma mémoire.
J’étais en fait assez tenté par la recherche en mathématiques. Frappé par tout ce que je viens de relater, je demandai à Schwartz : « Mais comment peut-on se lancer dans la recherche, quand on est aussi ignorant ? » Il me fit cette réponse (entre-temps, il était passé au tutoiement, qui lui était naturel) : « Tu en sais déjà suffisamment pour choisir un sujet et travailler avec l’aide d’une bonne boussole. » C’est vrai. Avec une bonne base et une bonne boussole, tout devient possible. La base, en l’occurrence le cours de Schwartz, malgré ou peut-être même à cause de son caractère foisonnant, nous l’avions. Avec elle, nous pouvions sans handicap approfondir n’importe quelle piste et aller chercher ce dont nous avions besoin pour y parvenir. La boussole, c’était le maître, ou éventuellement les maîtres. Il ne me fallut pas longtemps pour comprendre que ce principe est général.
Je voudrais terminer avec quelques remarques sur les conceptions et l’action de Laurent Schwartz relativement à l’enseignement de l’X. J’ai pu le suivre par de multiples conversations, mais aussi à travers les groupes de travail, auxquels j’ai été associé dès ma sortie de l’École, et ensuite en devenant maître de conférences en 1969, puis, en 1973-1974, professeur (détaché du corps des Mines) et président du département des sciences économiques (je le suis resté jusqu’en 1992 tout en exerçant par ailleurs mes fonctions de directeur du Centre d’analyse et de prévision au ministère des Affaires étrangères, puis de directeur de l’Ifri).
Sur l’énorme bouillonnement de réformes à la fin des années 1960, où d’ailleurs la notion de percolation prend tout son sens en l’occurrence sur un mode collectif (ce que les historiens appellent le mouvement des idées), on trouve bien sûr des éléments dans son autobiographie, avec cependant des inexactitudes sur les dates et sur le rôle des uns ou des autres, parce qu’il a travaillé de mémoire, sans vérifier les sources ni consulter les archives. Il appartiendra à de futurs historiens de remettre les choses en place, ce qui est aujourd’hui hors de mon propos et de ma portée.
Schwartz avait deux grandes ambitions. Il le dit clairement dans ses Mémoires et nous en parlait souvent à l’époque. L’une était la « régénération de la formation des ingénieurs », l’autre la formation de chercheurs. Il pensait que l’intérêt général commandait d’accroître le nombre des chercheurs issus de l’École. À ce sujet, on lui a fait un faux procès. Les conservateurs dénonçaient ce savant qui prétendait changer la culture polytechnicienne. Pour eux, les polytechniciens devaient « apprendre à apprendre », se préparer à « devenir les P-DG de demain… », et autres platitudes. Ce que disait Schwartz, c’était tout simplement qu’il devait y avoir une certaine proportion de chercheurs sortis de l’École. Pendant une partie du XIXe siècle, l’X avait donné à la France quelques-uns de ses meilleurs savants. Ampère, Cauchy, Fourier, Lagrange, Laplace, Legendre, Monge, Poisson et Poncelet y avaient enseigné. Au XXe siècle, l’École n’aura donné que deux prix Nobel (ce n’est qu’un critère parmi d’autres, mais il est significatif) : Henri Becquerel en 1903 (avec Pierre et Marie Curie) et Maurice Allais en 1988. Et encore le second a-t-il été couronné pour les sciences économiques.
Sur le plan de la recherche, l’objectif a été assez remarquablement atteint, et dès la « fameuse promotion 1963 », l’École a donné plusieurs mathématiciens du meilleur niveau international. Dès 1966, la création du centre de mathématiques a favorisé une évolution qui s’est progressivement étendue à toutes les disciplines, grâce à des personnalités comme Henri Piatier, directeur général adjoint au tournant des années 1960, et Pierre Vasseur, responsable des laboratoires.
S’agissant de la formation des ingénieurs, les choses étaient encore plus complexes. La recherche est, ou devrait être, une vocation, temporaire dans beaucoup de cas, définitive pour un petit nombre. La plupart des jeunes n’ont pas de vocation précise, tout juste des tendances ou des goûts pour certains types d’activité. La notion d’ingénieur n’a rien d’immédiat. La seule manière d’aborder la question était de diversifier les enseignements à l’intérieur de l’École et, en conséquence, les concours de recrutement en amont et les modes de classement en aval. En même temps se posaient les problèmes de l’allongement de la durée de la scolarité et de l’accroissement de l’effectif des promotions. Il s’agissait d’une véritable révolution culturelle, indispensable aux yeux des réformateurs comme Leprince-Ringuet, Schwartz, Ullmo ou Grison, et iconoclaste pour les conservateurs. Le mouvement en ce sens était amorcé bien avant 1968, mais les fameux « événements de mai 1968 » lui ont donné un coup d’accélérateur, non sans provoquer quelques débordements. Il fallut encore de nombreuses années et beaucoup d’efforts pour accomplir la mutation. Mais ceci est une autre histoire.
Sur le fond, je voudrais m’arrêter un instant sur le concept d’utilité d’un enseignement. Les professeurs se trouvent constamment confrontés à la question : à quoi cela sert-il ? La réponse, évidemment est que tout dépend de l’objectif. La plupart des malentendus entre enseignants et enseignés proviennent d’un désaccord implicite sur les objectifs. Et même dans le cas purement théorique d’un objectif bien déterminé, la combinaison appropriée des « facteurs de production », pour employer une métaphore d’économiste, n’est généralement pas unique. En vérité, on avance dans les études comme dans la recherche, avec une base et une boussole, avec cette difficulté que la direction est plus aléatoire. Un enseignement bien diversifié doit donc tenir compte à la fois des dispositions et des goûts de base des élèves (tel est plus mathématicien, tel autre est davantage physicien, etc.) et de l’impératif d’adaptation, donc de flexibilité, que l’évolution du monde a rendu de plus en plus nécessaire. À quoi j’ajouterai  c’est presque un corollaire  qu’une grande école doit développer l’esprit critique des ingénieurs-citoyens, d’où la place importante que les réformes successives ont faite à l’X au département « humanités et sciences sociales ».
Laurent Schwartz distinguait ce qu’il appelait l’« omnidisciplinarité » et la « pluridisciplinarité ». On pouvait évidemment être partisan à la fois de la diversification des enseignements et de l’accroissement du nombre des disciplines enseignées. Un bon polytechnicien devait se frotter à un large éventail de disciplines  mais un éventail adapté à chacun et tout de même suffisamment limité pour que chacun puisse approfondir sérieusement au moins l’une d’entre elles. Dans ces conditions, il était effectivement possible et même souhaitable d’accroître le menu total offert aux étudiants.
Ainsi Schwartz défendait-il, dès le début des années 1960, l’introduction de la biologie. Ce n’était évidemment pas seulement parce qu’il se passionnait pour l’entomologie et pour les papillons, mais il avait compris que la biologie serait le grand domaine des décennies suivantes. Il pensait que dans les sciences de la vie aussi, l’École polytechnique devait et pouvait fournir des chercheurs. Et tel fut bien le cas.
Autre idée iconoclaste dans le contexte de l’époque : Schwartz voulait jeter des ponts entre l’Université et les grandes écoles. Il était favorable à l’idée alors très discutée de créer une sorte d’université d’élite en regroupant plusieurs établissements, une idée qui serait caressée un peu plus tard pour justifier la décision, prise en 1965, de transférer Polytechnique. Mais le projet initial n’eut guère de suite, de sorte que l’École s’est finalement retrouvée seule sur le plateau de Palaiseau… Schwartz voulait également que les polytechniciens puissent se mesurer à l’Université en les obligeant à passer des certificats de licence, comme les normaliens devaient le faire. La proposition avait bien sûr suscité un tollé. Elle répondait à ses vues sur la sélection, sur ce que l’on appellerait aujourd’hui le benchmarking, c’est-à-dire l’évaluation et donc la comparaison, mais aussi avec sa conviction qu’il était scandaleux qu’un élève puisse obtenir le diplôme de l’École polytechnique en n’ayant fourni d’effort que pour le concours d’entrée. Tel est le point sur lequel s’est focalisée la crise de 1977, à la suite d’un jury particulièrement laxiste. Schwartz avait publié un article dans Le Monde, dans lequel il dénonçait le « gaspillage des cerveaux », suscitant l’ire des autorités. La victime expiatoire fut, hélas, Henri Piatier. J’ajouterai que, ayant pendant des années siégé dans les jurys de l’École, je n’ai cessé de m’insurger moi-même contre le fait qu’il soit effectivement possible d’avoir le titre d’ancien élève de l’École polytechnique en n’y ayant rien fait et, avec cela, en ayant été logé, nourri et rémunéré.
Laurent Schwartz n’avait pas une conception étriquée de l’activité scientifique. Ainsi s’est-il montré extraordinairement ouvert, en 1968, à l’idée d’élever l’économie au même rang que les disciplines principales traditionnelles (mathématiques, physique, chimie, mécanique). Je me souviens tout particulièrement d’un séminaire d’économie mathématique que je donnais avec Jean-Pierre Aubin en 1969-1970, à l’origine de mon premier livre . Schwartz y avait participé de bout en bout, et ses observations m’avaient été infiniment précieuses. Le sujet ne lui était pas inconnu, puisqu’il avait accepté de participer une dizaine d’années plus tôt au jury de la thèse de Gérard Debreu sur « la théorie de la valeur », laquelle, avec d’autres travaux, devait conduire son auteur au prix Nobel de sciences économiques en 1983. Schwartz m’avait d’ailleurs encouragé à aller travailler avec ce pionnier à Berkeley. Je lui dois, ainsi qu’à Jean Ullmo, à Henri Piatier et quelques autres, ma nomination comme professeur d’« exercice complet » en 1973, à une époque où les professeurs « titulaires », toutes disciplines confondues, se comptaient sur les doigts des mains, ou presque. Le soutien qu’il m’a constamment apporté a été déterminant pour l’élan que j’ai pu donner au département de sciences économiques, à la suite de Jean Ullmo, son premier président.
Le moment est venu de conclure. Je n’ai jamais coupé le fil avec Laurent Schwartz. Ces dernières années, je continuais de le voir occasionnellement à l’Institut de France. Jusqu’à tout récemment, l’Académie des sciences et l’Académie des sciences morales et politiques siégeaient toutes les deux le lundi. Je me souviens avec précision de ma dernière visite dans l’appartement de la rue Pierre-Nicole, en février 1999. Rien n’avait changé depuis ce jour du début des années 1960 où mon professeur m’avait fait les honneurs de sa collection de papillons. Comme alors, il m’avait accueilli à bras ouverts, avec sa femme Marie-Hélène. Nous avions échangé des souvenirs, parlé de ses Mémoires, de la façon dont il avait mené ce projet à bien. Je lui avais parlé de ma « cristallisation » de 1963. Cette histoire lui avait plu. Puis la conversation s’était orientée sur un aspect fondamental de la philosophie des mathématiques. Schwartz était résolument platonicien. Comme Charles Hermite et bien d’autres, il croyait que les mathématiciens n’inventent rien, mais qu’ils sont parfois autorisés à découvrir l’harmonie d’un monde dont l’existence est indépendante de l’esprit humain . De la même manière, il croyait que les lois de la morale sont aussi universelles que celles de la physique. Dans les deux cas, j’ai employé le verbe croire, parce que nous nous situons dans un ordre métaphysique et sur le registre d’une foi, non pas détachée, mais prodigieusement incarnée. On comprend pourquoi Schwartz préférait parler de découverte plutôt que d’invention à propos des mathématiques, et l’on pourrait bien sûr méditer sur le terme le plus juste dans d’autres domaines de la connaissance. Certains savants, comme Jean-Pierre Changeux, considèrent les mathématiques comme une pure construction de l’imagination. Mais les exemples qu’ils avancent à l’appui de leur thèse sont rarement de nature à ébranler la conviction d’un platonicien. Ainsi, dans cette conversation de février 1999, Schwartz s’étonnait-il de la distinction, radicale pour Changeux, entre nombres réels et nombres complexes, les premiers  selon le biologiste  étant bel et bien réels comme leur nom l’indiquerait, et les seconds imaginaires comme leur ancien nom le suggérait. En fait, les nombres réels sont aussi imaginaires que les nombres complexes, et les nombres complexes aussi réels que ceux ainsi qualifiés. Les uns comme les autres résultent d’une construction purement mathématique, construction peut-être même encore plus audacieuse s’agissant des réels que des complexes. C’est le même type de travail architectural qui est à l’œuvre dans le passage des fonctions aux distributions, et chaque personne doit nécessairement effectuer un travail psychologique plus ou moins long d’appropriation ou d’incarnation avant de ressentir l’évidence de la « réalité » des « réels » e ou π, de l’« imaginaire » i ou de la distribution . Tout cela nous ramène au thème de la cristallisation. Du point de vue de la sensibilité immédiate, seule s’impose la « réalité » des nombres entiers, et encore sait-on aujourd’hui combien d’efforts il a fallu à l’humanité pour en dégager clairement la notion. Ce côté laborieux se retrouve d’ailleurs quand on réfléchit à leur axiomatisation. Pour enfoncer le clou, Schwartz observait que l’ensemble des nombres réels « définissables » était démontrable, et que l’ensemble de tous les théorèmes qui seront jamais démontrés est fini ! Si je me suis un peu attardé sur ces questions, c’est que j’ai toujours été convaincu de l’utilité et même de la nécessité de faire une place, dans l’enseignement de l’École polytechnique, à l’histoire et à la philosophie des sciences.

Une phrase, dans les Mémoires de Laurent Schwartz, m’a particulièrement touché, ne serait-ce que parce qu’elle entre en résonance avec mes propres travaux sur le thème de l’action . Je le cite : « J’ai toujours voulu “changer le monde”, changer la vie. Je suis resté un réformateur que toute structure défectueuse et sclérosée tracasse . » C’est magnifique. Cette passion réformatrice, et donc subversive, comme il le remarquait volontiers, il l’a d’abord vécue sur le mode trotskiste, ce qui n’était bien sûr que l’une des voies possibles, et ce fut la sienne pendant onze ans. Cette passion, il l’a mise au service de l’Université et de l’École polytechnique, mais aussi dans ses engagements politiques. Ainsi écrit-il dans ses Mémoires, non sans une certaine fraîcheur : « Je suis profondément convaincu d’avoir été, par ma seule personne, par mes activités acharnées et débordantes, un facteur non négligeable de la paix en Algérie, tandis que dans le même temps j’œuvrais à la modernisation de l’École polytechnique. Un facteur, rien d’autre, mais plus qu’une goutte d’eau dans l’océan . » On pourrait dire la même chose de toute son œuvre. Perpétuel combattant, il était très respectueux des personnes. Je ne l’ai jamais entendu parler médiocrement de quelqu’un. Il ne s’intéressait qu’à de vraies causes. Cela, c’est tout à fait exceptionnel. Il avait évidemment une haute conscience morale. Il était de ces athées-croyants qui donnent l’impression de ne jamais douter. Il avait le culte de l’homme, de sa dignité. Toute sa vie, il aura assumé ses convictions de manière inébranlable et courageuse, prenant parfois de véritables risques, même physiques. Et, s’il a aussi fortement marqué ceux qui l’ont approché, ce n’est pas seulement parce qu’il fut un immense mathématicien et un professeur sublime. C’est aussi parce qu’il portait en lui une vérité désintéressée. Et l’on allait vers lui comme on va vers la lumière.